Z tematem ułamków zwykłych uczniowie spotykają się w szkole podstawowej po raz pierwszy już w klasie drugiej, kiedy to mowa jest o podziale całości na połowy i ćwiartki. I właśnie w tym momencie pojawia nam się już pierwsza z interpretacji ułamka. Mianowicie: podział liczby lub wielkości na jednakowe części, czyli operatywne rozumienie ułamka. W literaturze metodycznej mówi się tu o czynności podziału lub wyniku podziału. W praktyce jest to suma jednakowych części podziału, np.: pokazanie ułamka na kwadracie, kole, prostokącie itp.

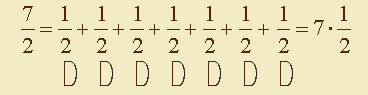
W przedstawionym powyżej przykładzie wynik odczytamy jako siedem połówek koła.
Ułamek w szkole podstawowej interpretowany jest również jako iloraz dwóch liczb całkowitych, z których druga jest różna od zera, czyli:

oznacza wynik dzielenia.

Takie ujęcie, oznacza rozpatrywanie ułamka w aspekcie arytmetycznym. Oprócz tego aspektu wyróżnia się również aspekt algebraiczny, czyli ułamek jako wynik rozwiązywania równania, np.:

Bardzo czytelnym i ciekawym dla uczniów jest też aspekt miarowy ułamka polegający na tym, że ustalamy jednostkę miary oraz wielkość mierzalną, np.: mamy odcinek AB i jednostkę e. Zadaniem ucznia jest sprawdzić ile razy jednostka miary mieści się w wielkości mierzonej, lub jaką część tej jednostki stanowi. U nas będzie to ułamek , co prezentuje poniższy rysunek:

W klasach młodszych, ale nie tylko, warto przy omawianiu ułamków posłużyć się osią liczbową. Uczeń powinien wiedzieć, że ułamki również można zaznaczać i że danemu ułamkowi odpowiada dokładnie jeden punkt na osi liczbowej, np.:

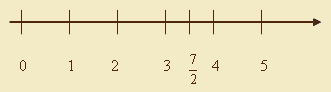
Wszystkie te interpretacje występują w nauczaniu matematyki, ale nie jednocześnie. W nauczaniu ułamków musi być zachowana zasada stopniowania trudności. Najpierw należy nauczać podziału jednostki na części i miarę, potem sumę jednakowych części, następnie interpretację ułamka jako ilorazu, a na samym końcu ułamek jako reszta pozostała z dzielenia dwóch liczb.

Wśród narzędzi dydaktycznych stosowanych w nauczaniu ułamków można wyróżnić:

• diagramy kołowe,
• oś liczbową,
• graf,
• kartoniki i nożyczki potrzebne do ich podziału.

Na koniec należy podkreślić, że ułamki zwykłe są tematem dość szerokim, dającym nauczycielowi wiele możliwości interpretacji, od której zależy też, czy uczeń zrozumie i polubi ten niezwykle ważny dział matematyki.

Więcej:

• Dróbka N., Szymański K., Matematyka w szkole podstawowej, WNT, Warszawa 1996.
• Jeleński S., Lilavati, WSiP, Warszawa 1992.
• Lewicka H., Rosłon E., Matematyka wokół nas, Podręcznik dla klasy 6, WSiP, Warszawa 2001.
• Zaremba D., Sztuka nauczania matematyki, Gdańskie Wydawnictwo Oświatowe, Gdańsk 1993.